Olá, meu povo!
Já comentei diversas vezes aqui mesmo no blog que muitas bancas cobram dos candidatos conhecimento de dois ou mais assuntos para a resolução de uma única questão. Veremos um exemplo disso, onde a Fundação Cesgranrio, na prova de Administrador Júnior da Petrobrás, realizada em 2010, cobrou Teoria dos Conjuntos e Probabilidade na mesma questão.
Em um posto de combustíveis entram, por hora, cerca de 300 clientes. Desses, 210 vão colocar combustível, 130 vão completar o óleo lubrificante e 120 vão calibrar os pneus. Sabe-se, ainda, que 70 colocam combustível e completam o óleo; 80 colocam combustível e calibram os pneus e 50 colocam combustível, completam o óleo e calibram os pneus. Considerando que os 300 clientes entram no posto de combustíveis para executar uma ou mais das atividades acima mencionadas, qual a probabilidade de um cliente entrar no posto para completar o óleo e calibrar os pneus?
(A) 0,10
(B) 0,20
(C) 0,25
(D) 0,40
(E) 0,45
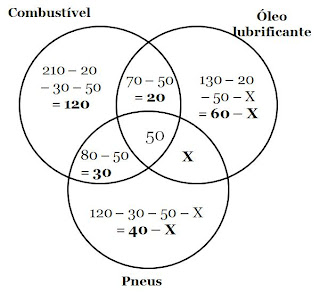
Primeiro, vamos montar o Diagrama de Venn, onde ‘x’ será a intersecção entre completar o óleo e calibrar os pneus (valor que não foi informado pela questão). Vou montar a figura e depois explico o que fiz, ok?
Sempre começamos pela intersecção, certo? Depois, preenchemos as intersecções entre 2 conjuntos, diminuindo de cada uma o valor da intersecção das 3. Ao final, preenchemos a parte ‘isolada’, diminuindo todas as intersecções.
Pronto! Agora, é só somar todos os valores e igualar a 300 (total de clientes). Fica assim:
110 + 60 – x + 40 – x + 20 + 30 + x + 50 = 300
310 – x = 300
x = 10
Como temos 50 clientes que, além de colocar combustível, COMPLETA O ÓLEO e CALIBRA OS PNEUS (intersecção dos 3 conjuntos), enão são, ao todo, 60 clientes.
Agora, utilizando a fórmula da Probabilidade, temos:
Resposta correta: letra B.
Faltam 171 questões!
Beijo no papai e na mamãe,
PH




0 comments:
Postar um comentário